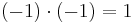−1 (number)
| −1 | |||
|---|---|---|---|
| Cardinal | −1, minus one, negative one | ||
| Arabic | −١ | ||
| Chinese numeral | 负一,负弌,负壹 | ||
| Bengali | ô১ | ||
| Binary (byte) |
|
||
| Hex (byte) |
|
||
In mathematics, −1 is the additive inverse of 1, that is, the number that when added to 1 gives the additive identity element, 0. It is the negative integer greater than negative two (−2) and less than 0.
Negative one has some similar but slightly different properties to positive one.[1]
Negative one bears relation to Euler's identity since 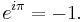
In computer science, −1 is a common initial value for integers and is also used to show that a variable contains no useful information.
Contents |
Algebraic properties
Multiplying a number by −1 is equivalent to changing the sign on the number. This can be proved using the distributive law and the axiom that 1 is the multiplicative identity: for x real, we have
where we used the fact that any real x times 0 equals 0, implied by cancellation from the equation
In other words,
so (−1) · x is the arithmetic inverse of x, or −x.
Square of −1
The square of −1, i.e. −1 multiplied by −1, equals 1. As a consequence, a product of negative real numbers is positive.
For an algebraic proof of this result, start with the equation
The first equality follows from the above result. The second follows from the definition of −1 as additive inverse of 1: it is precisely that number that when added to 1 gives 0. Now, using the distributive law, we see that
The second equality follows from the fact that 1 is a multiplicative identity. But now adding 1 to both sides of this last equation implies
The above arguments hold in any ring, a concept of abstract algebra generalizing integers and real numbers.
Square roots of −1
The complex number i satisfies i2 = −1, and as such can be considered as a square root of −1. The only other complex number x satisfying the equation x2 = −1 is −i. In the algebra of quaternions, containing the complex plane, the equation x2 = −1 has an infinity of solutions.[2]
Exponentiation to negative integers
Exponentiation of a non-zero real number can be extended to negative integers. We make the definition that x−1 = 1/x, meaning that we define raising a number to the power −1 to have the same effect as taking its reciprocal. This definition then extended to negative integers preserves the exponential law xaxb = x(a + b) for a,b non-zero real numbers.
Exponentiation to negative integers can be extended to invertible elements of a ring, by defining x−1 as the multiplicative inverse of x.
Computer representation
There are a variety of ways that −1 (and negative numbers in general) can be represented in computer systems, the most common being as two's complement of their positive form. Since this representation could also represent a positive integer in standard binary representation, a programmer must be careful not to confuse the two. Negative one in two's complement could be mistaken for the positive integer 2n − 1, where n is the number of digits in the representation (that is, the number of bits in the data type). For example, 111111112 (binary) and FF16 (hex) each represents −1 in two's complement, but represents 255 in standard numeric representation.
See also
References
- ^ Mathematical analysis and applications By Jayant V. Deshpande, ISBN 1842651897
- ^ http://mathforum.org/library/drmath/view/58251.html
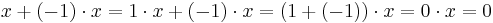
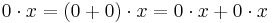
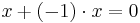
![0 =-1\cdot 0 =-1\cdot [1%2B(-1)]](/2012-wikipedia_en_all_nopic_01_2012/I/9652c1e53be68a5c8d9764987ba960a2.png)
![0 =-1\cdot [1%2B(-1)]=-1\cdot1%2B(-1)\cdot(-1)=-1%2B(-1)\cdot(-1)](/2012-wikipedia_en_all_nopic_01_2012/I/1d285c708caa2574cd5ea75c99544a60.png)